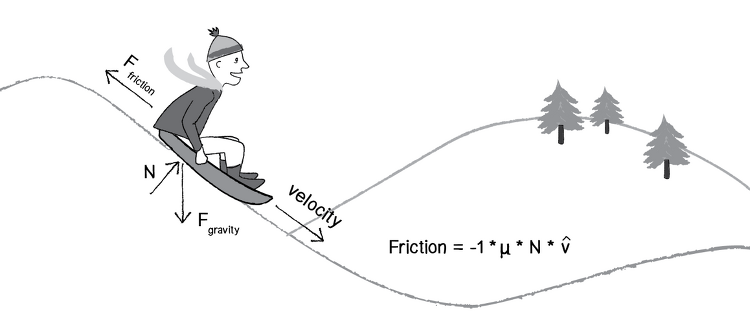
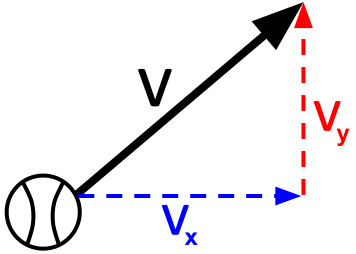
마찰력(Friction)은 두 물체의 접촉면 사이에서 물체의 운동을 방해하는 힘이다. 그림에서처럼, 썰매와 눈이내린 언덕사이의 마찰력때문에 이 썰매는 언젠가 멈추게 될 것이다. 그러면 프로그래밍에서 이 썰매를 어떻게 멈추게 할 것인가? 이 글에서는 두 물체가 상대적으로 움직이면서 문질러질때 발생하는 운동 마찰력만을 다루려고 한다. 마찰력의 공식은 다음과 같다. 이제 마찰력을 크기와 방향 두 성분으로 나누어 어떻게 계산하면 되는지 살펴볼 것이다. 먼저 방향이다. 마찰력의 방향은 물체에 작용하고 있는 힘과 반대로 작용한다. 공식에서 v는 속도 벡터를 의미하는데, 속도 벡터에 -1을 곱해 방향을 반대로 틀었다. // 벡터의 크기 구하기 function getMagnitude(x, y) { return Math..