삼각비

각 A의 크기가 같은 세 직각 삼각형 ABC / ADE / AFG은 모두 닮은 도형이다. 이 닮은 도형들의 대응변 길이의 값은 항상 그 비율이 같게 된다. CB / AB = ED / AD 이런식으로... 이렇게삼각형의 각 변에 대해서 두 변의 길이의 비례값을 구할 수 있는데, 이것이 sin, cos, tan이다. sin A, cos A, tan A를 모두 통틀어 각 A에 대한 삼각비라고 한다.

유치하지만 이렇게 sin, cos, tan을 외웠었지...아무튼 각 삼각비가 어느 변들의 비례를 말하는 것인지만 기억하면 된다. 특수각 30° / 45° / 60°도에대한 삼각비 값이 정리된 표를 심심찮게 볼 수 있지만 아래처럼 계산하기 편한 삼각형을 만들어서 특수각들에 대한 sin, cos, tan 값을 도출해낼 수 있다.
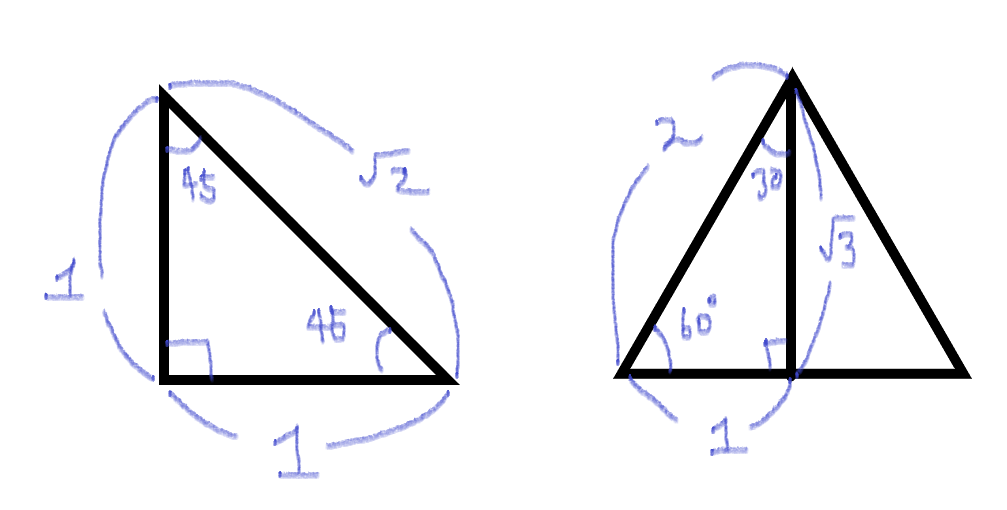
나머지 0°와 90°에대해서도 각도가 점점 0°에 수렴하거나 90°도 커지는 것을 보면 sin, cos, tan을 알 수 있다.

삼각함수와 그래프

삼각비는 예각에 대해서만 보았지만, 이 삼각비의 각을 일반각으로 확장시켜 식을 세운 것이 삼각함수다. sinθ = y/r 이니 이것을 y에 대한 식으로 정리해보면 y = sinθr 이되는데, 단위 원에서 r=1 이므로 y = sinθ가된다. θ값이 커짐에 따른 y의 값을 좌표평면위에 부드러운 곡선으로 나타낸 것이 sinθ의 그래프다. cosθ의 그래프도 같은 방법이다.


sin 함수와 cos 함수에서 θ를 x, 그리고 f(θ)를 y로 나타내기로 하면, 두 함수 y = sinx, y = cosx는 일정한 주기를 가지고 반복됨을 알 수 있는데, 당연히 한바퀴 돈 2π다. 반면, y = tanθ의 그래프는 다음과 같이 그려지게 되는데, 180°지점에서 다시 0이되어 tan 함수는 그 주기가 π다.

삼각함수를 이용해 캔버스에 물결 그리기

부드러운 물결같은 선을 그리려고 할때 삼각함수를 응용할 수 있다. 전체 소스는 아래에 첨부되어있다. 위에 그린 gif 처럼 sin 그래프에서 θ값을 계속 늘려가면서 path를 그려 파동을 만들었다. 최대 y값을 낮추면 잔잔한 물결처럼 그려지게 된다. 알아보기 쉽게하기 위해 X축도 추가해두었다.
<!DOCTYPE html>
<meta name="viewport" content="width=device-width,initial-scale=1">
<style>
canvas {
background: #eeeeee;
}
</style>
<body>
<canvas id="canvas" width="500" height="320"/>
</body>
<script>
var canvas = document.getElementById('canvas');
drawAxis(); // 축 그리기
drawSine(canvas.height / 2); // sine 그래프 그리기
function drawAxis() {
var context = canvas.getContext("2d");
context.beginPath();
// x Axis;
for (var pX = 0; pX < canvas.width; pX++) {
context.lineTo(pX, canvas.height / 2);
}
context.strokeStyle = "#333";
context.stroke();
}
// 최대 y높이가 MAX 값을 가지는 sine 그래프 그림
function drawSine(max) {
var context = canvas.getContext("2d");
context.beginPath();
var degree = 0;
for (var degree = 0; degree < canvas.width; degree+=5) {
var pX = degree; // 캔버스 길이만큼 그리므로
var pY = (canvas.height / 2) + (Math.sin(degToRad(degree)) * max);
context.lineTo(pX, pY);
}
context.lineWidth = 3;
context.strokeStyle = "#11AD55";
context.stroke();
}
function degToRad(degree) {
return Math.PI / 180 * degree
}
</script>
</html>
참고자료
'프로그래밍 > 수학' 카테고리의 다른 글
| 프로그래밍을 위한 수학 - 벡터 기초 (0) | 2022.08.28 |
|---|---|
| 프로그래밍을 위한 수학 - X축과 직선이 이루는 사이각 구하기 (0) | 2022.08.27 |
| 컴퓨터가 2의 보수 표현을 사용하는 이유 (0) | 2022.02.04 |
| 특정 범위의 값을 퍼센트(percentage)로 변환하기 (0) | 2022.01.13 |
| 프로그래밍을 위한 수학 - 호도법 (0) | 2022.01.09 |