180도면 180도지! 왜 각도를 지맘대로 쓰세요??

일반적으로 우리가 사용하는 0 ~ 360도로 각도를 표현하는 방법은 60분법(Degree)이다. 대부분의 프로그래밍 언어에서는 삼각함수를 다룰때 매개변수로 Radian을 받는다. 이처럼 각도를 Radian으로 표기하는 방법을 호도법이라고 한다. 호도법을 이용하면 °같은 단위표기없이 숫자로만 각도를 표시할 수 있기때문에 계산이 편하다는 이점이 있다.
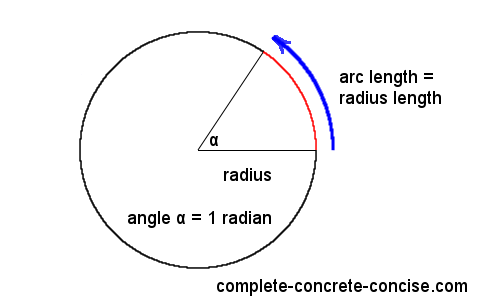
호도법
호도법은 원의 호의 길이를 이용해 각도를 나타내는 방법이다. 반지름의 길이가 r인 원에서, 길이가 r인 호에대한 중심각의 크기를 a°라고 하면 호의 길이는 중심각의 크기에 정비례 하므로 다음과 같이 계산할 수 있다.
원주율 π는 원의 둘레가 지름의 몇 배인지나타내므로, 원의 둘레는 2r * π이다.
그러면 비례식을 다음과 같이 세울 수 있는데, 정리하면...중심각 크기 a°는 반지름 r의 길이와 관계없이 일정함을 알 수 있다.
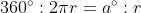
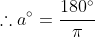
이 a°를 1Rad(Radian)이라고 하고, 호도법에서는 이렇게 Radian을 단위로 각의 크기를 나타 낸다.

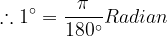
1°에대해서는 이렇게 표현이 될 수 있는데, 일반적으로 Radian은 생략한다. 1°에 대한 Radian값이 구해졌으니 60분법으로 표기한 각도를 호도법으로 바꿔보면 이렇게 된다.
| 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3/2π | 2π |
호도법으로 일반각 계산
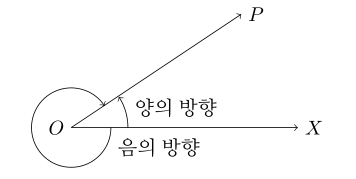
두 반직선 OX, OP로 이루어진 도형 XOP에서 XOP가 나타내는 각의 크기는 다음과 같이 무수히 많다.
420° = 360° * 1 + 60°
-660° = 360° * -2 + 60°
-1020° = 360° * -3 + 60°
위 3개의 각도들 모두 그냥 돌고돌아 60°를 나타내는데,
이 모든 각들은 다음과 같은 식으로 나타낼 수 있다. (n은 정수)
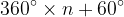
이때 60°를 동경 OP가 나타내는 일반각 a° 이라고 한다. 따라서 0° <= a° <= 360° 가되고,
호도법으로는 a° = θRad라고 표기할 수 있으므로 0 <= θ <= 2π이다.
참고자료
'프로그래밍 > 수학' 카테고리의 다른 글
| 프로그래밍을 위한 수학 - 벡터 기초 (0) | 2022.08.28 |
|---|---|
| 프로그래밍을 위한 수학 - X축과 직선이 이루는 사이각 구하기 (0) | 2022.08.27 |
| 컴퓨터가 2의 보수 표현을 사용하는 이유 (0) | 2022.02.04 |
| 특정 범위의 값을 퍼센트(percentage)로 변환하기 (0) | 2022.01.13 |
| 프로그래밍을 위한 수학 - 삼각비, 삼각함수 그래프 (0) | 2022.01.09 |